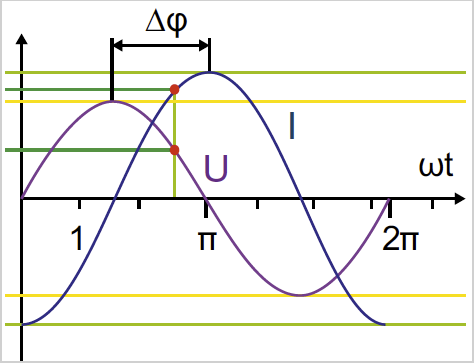
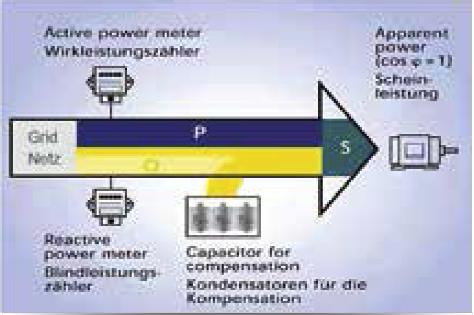
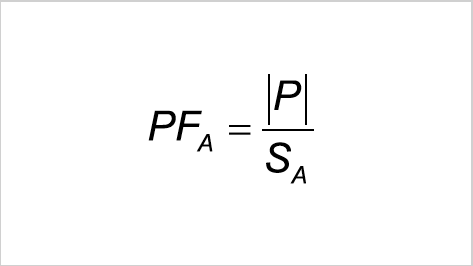
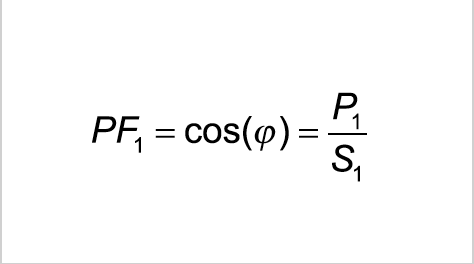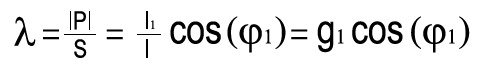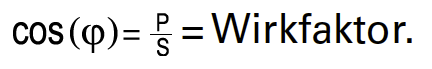Blindleistung wird zur Erzeugung elektromagnetischer Felder von Maschinen wie z.B. Drehstrommotoren, Transformatoren, Schweißanlagen etc. benötigt. Da sich diese Felder kontinuierlich auf- und wieder abbauen, pendelt die Blindleistung zwischen Erzeuger und Verbrauchsmittel. Sie kann im Gegensatz zur Wirkleistung nicht genutzt, d.h. in eine andere Energieform umgewandelt werden und belastet das Stromversorgungsnetz und die Erzeugeranlagen (Generatoren und Transformatoren). Ferner müssen alle Energieverteilungsanlagen für die Bereitstellung des Blindstroms größer ausgelegt werden.
Daher ist es zweckmäßig, nahe am Verbraucher die entstehende induktive Blindleistung durch eine entgegenwirkende kapazitive Blindleistung von möglichst gleicher Größe zu reduzieren. Diesen Vorgang nennt man kompensieren. Bei der Kompensation verringert sich der Anteil der induktiven Blindleistung im Netz um die Blindleistung des Leistungskondensators oder der Kompensationsanlage (BLK). Die Erzeugeranlagen und Energieübertragungseinrichtungen werden damit vom Blindstrom entlastet. Die Phasenverschiebung zwischen Strom und Spannung wird reduziert oder im Idealfall bei Leistungsfaktor 1 auch ganz eliminiert.
Der Leistungsfaktor (Power Factor) ist ein Parameter, der von Netzstörungen wie Verzerrung oder Unsymmetrie beeinflusst werden kann. Er verschlechtert sich mit fortschreitender Phasenverschiebung zwischen Strom und Spannung und mit zunehmender Verzerrung der Stromkurve. Er ist definiert als Quotient aus dem Betrag der Wirkleistung und Scheinleistung und ist somit ein Maß für die Effizienz, mit der eine Last die elektrische Energie nutzt. Ein höherer Leistungsfaktor stellt also eine verbesserte Nutzung der elektrischen Energie und letztendlich auch einen höheren Wirkungsgrad dar.
Da sich bei Oberschwingungsbelastung kein einheitlicher Phasenverschiebungswinkel angeben lässt, dürfen Leistungsfaktor λ und der häufig verwendete Wirkfaktor cos(φ1) nicht gleichgesetzt werden. Ausgehend von der Formel (Grafik 1)
mit I1 = Grundschwingungseffektivwert des Stroms, I = Gesamteffektivwert des Stroms, g1 = Grundschwingungsgehalt des Stroms und cos(φ1) = Verschiebungsfaktor erkennt man, dass nur bei sinusförmiger Spannung und Strom (g = 1) der Leistungsfaktor λ gleich dem Verschiebungsfaktor cos(φ1) ist. Somit ist ausschließlich bei sinusförmigen Strömen und Spannungen der Leistungsfaktor λ gleich dem Kosinus des Phasenverschiebungswinkels φ und wird definiert als (Grafik 2)
Grafik 1
Grafik 2
