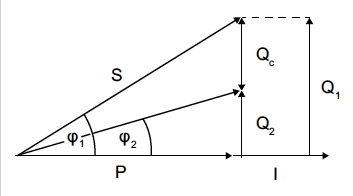
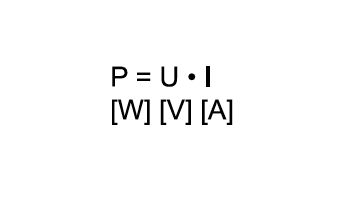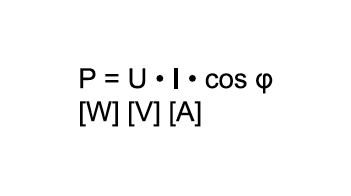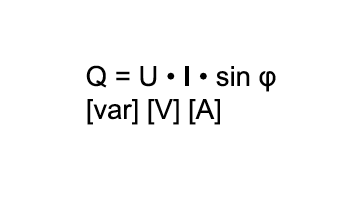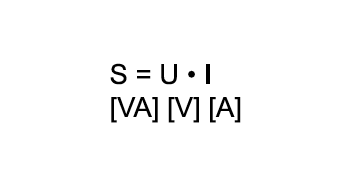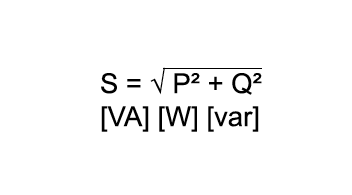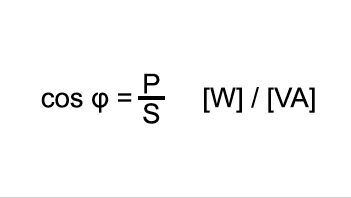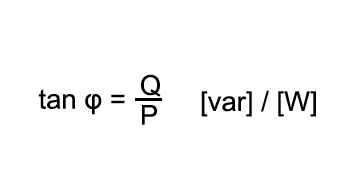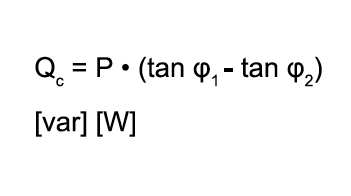Eine rein ohmsche Last tritt in der Praxis selten auf. Häufig kommt zusätzlich eine induktive Komponente dazu. Dies gilt für alle Verbraucher, die zur Funktion ein magnetisches Feld benötigen (z.B. Motoren, Transformatoren etc.). Der verwendete Strom, der zum Aufbau und Umpolen des magnetischen Feldes benötigt wird, verbraucht sich nicht, sondern pendelt als Blindstrom zwischen Generator und Verbraucher.
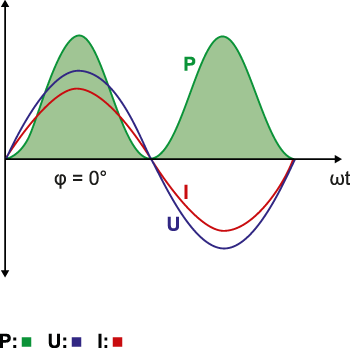
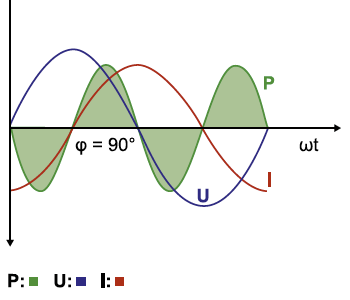
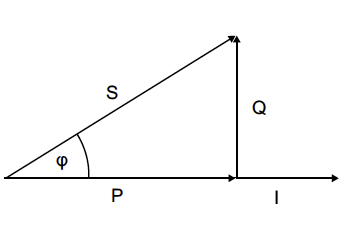
Eine Phasenverschiebung tritt auf, d.h., die Nulldurchgänge von Spannung und Strom sind nicht mehr deckungsgleich. Bei induktiver Last läuft der Strom der Spannung nach, bei kapazitiver Last ist das Verhältnis genau umgekehrt. Berechnet man jetzt die Augenblickswerte der Leistung (P = U x I), entstehen immer dann negative Werte, wenn einer der beiden Faktoren negativ wird.
Beispiel:
Phasenverschiebung φ = 45° (entspricht einem induktiven cos φ = 0,707). Die Leistungskurve überlagert in den negativen Bereich.